Size, Democracy & Political Control

Size, Democracy & Political Control:

Measuring the effect of community size on local political autonomy

“…The institutions of a township are to freedom what primary schools are to science; they put it within reach of the people; they make them taste its peaceful employ and habituate them to making use of it. Without the institutions of a township a nation can give itself a free government, but it does not have the spirit of freedom.” Alexis de Tocqueville, Democracy in America

If democracy in government is understood as the personal involvement of citizens in the functions and power of governance, then the strongest democracy can be found where power and the responsibility of decision making are the least delegated by citizens to their representatives, and where individuals are most able to personally interact with and control the levers of government. This is reflected in Frank Bryan's “Real Democracy” (Bryan, 2004) and his body of work on town meetings in Vermont; smaller political entities lead to more and better participation by citizens in the work of government, and as important decisions are delegated up the pyramid of representatives the interest of citizens and their civic participatory ethic declines. As the populations of polities grow larger the decisions, resources and the meat of governance become centralized in the pursuit of efficiency, predictability and convenience. Bryan’s work demonstrates that this leads to a reduction in the involvement of citizens in the works of government, the definition of weaker democracy. Large polities suffer from the inherent difficulties of remoteness; a large, central government must maintain a one-size-fits-all approach to governance, an approach that unavoidably fails to reflect differences in values and needs between constituents.  The democratic ideal, then, may be small political units exercising meaningful decision-making authority that reflects the needs and interests of its relatively few constituents. This is the premise and foundation of federalism, and a conclusion that is the subject of widespread agreement. (Bell, Brunori & Youngman, 2010).

The link between democracy and decision-making authority is important; if voting and deliberative bodies are the forms of democratic governance, then the substance is in the scope of power wielded by the democratic process. To get to a fundamental understanding about the variation in democracy between large and small political units, then, we need to connect participatory measurements of democracy with some analysis of government in action – power exercised, decisions made. But decision-making authority is hard to measure; it could be counted by votes taken, bills passed, regulations issued or myriad other metrics of bureaucratic machinations. The best measurements are perhaps the hardest to tease out – positive outcomes, satisfied constituents, fiscal efficiency, etc. While it’s possible to empirically study these measurements, they are beyond the scope of this project. Other research has delved into the fiscal and legal conditions that delineate and foster local autonomy, or studied the social and political ramifications of local government from the perspective of its impact on national political involvement. Yet on the social conditions for democracy and local autonomy, few connections appear to have been made. (Vetter, 2007).

In this paper I attempt to test a simple argument; democracy works better in small communities, and if this superior democracy can be translated into improved power and standing for local governments, then those states in the U.S. with a higher proportion of citizens living in small communities should rate higher on measurements of local political power and autonomy.

Independent Variable

While there are many possible definitions for small communities in the U.S., for this report I've selected the United States Census measurement of rural places. The decennial Census defines rural communities as those with 2500 or fewer residents, and provides the data by state. I've used the proportion of the state population living in communities with 2500 or fewer residents as the independent variable; this measure controls for size and is an adequate proxy for small communities.

Dependent Variable

Local autonomy is a term with definitions that vary by use; for the purpose of this paper, I adopt the descriptions used by Wollman et al (2008) and Clark (1984). Local autonomy is understood as the importance of the role played by the local government in the economy and intergovernmental relations, the degree of initiative held by local governments to enact limits on the behavior of residents, and the scope of freedom from constraint and supervision by state authorities. 

Empirically measuring the degree of local political independence, or autonomy, is a task with no consensus method. In some studies the Dillon's rule status of particular states are used as a distinguishing feature. (Richardson, 2011) Dillon's rule, outlined in 1868 by Iowa judge John Dillon, is the principle that local governments have no original authority; any political power they may possess or wield is derived solely from the sufferance of the state. Since this principle of jurisprudence was described, some states have carved out exceptions by establishing home rule provisions either by statute or in state constitutions. The scope, consistency and degree of authority provided by home rule exceptions varies greatly by state and over time. More importantly, using a Dillon's Rule dichotomy provides limited correspondence with other measures of local government autonomy. (Richardson, 2011).

Another measure, the Stephens Centralization Index, was first published in 1974 and updated in 2002. In his 1974 paper, G. Ross Stephens  “[...] devised a composite index of state centralization using the following three components that reflect the relative distribution of power between the state and local governments: (1) financial responsibility, or which level pays for goods and services; (2) determination of the level that delivers each of fifteen major functional activities; and (3) distribution of public personnel between levels modified by the relative labor intensity of different services rendered by state and local governments.” (Stephens & Wikstrom, 2007).

The Local Autonomy Index, developed by Harold Wollman et al (2008), is the measurement I will be using to represent the degree of government power and control devolved to the local level. Wollman, of The George Washington Institute of Public Policy (GWIPP) group, identified three dimensions of local autonomy:

1.                  Local Government Importance: This dimension analyzes the importance of the actions a local government can take and the decisions it is free to make, and its position relative to other levels of government.

2.                  Local Government Discretion: This dimension analyzes local government freedom to act, focusing on fiscal discretion, functional and legal responsibility, and their ability to raise and spend money without imposed constraints.

2.                  Local Government Capacity: While the authors conceptually defined "capacity" to include a variety of resources, competencies and professional qualifications, they operationally defined it as "stability and diversity of revenue sources." In effect, this measures the freedom and flexibility of a local government unit with respect to its ability to spend money.

The index is a combination of standardized measures of each dimension. The authors of the index report a correlation with the Stephens Centralization index (or rather, a standardized inverse) of

r = .673, suggesting that it is unnecessary to combine or otherwise manipulate the separate indices. (Wollman et al, 2008).

Control Variables

To isolate the effect, if any, of community size on local autonomy I control for elements of what collectively represent social conflict. Tension and competition between ethnic, social and economic groups may be a strong impetus for local autonomy; different demands for social services, different political values, and other social distinctions might push states to devolve decision-making regardless of community size.

The first control is the percentage of the population of a state living in the two largest cities. I suggest that the presence of a strong urban political center, such as New York or Chicago, will result in a strong rating for local autonomy because of the gravitational pull such large cities have on political devolution. There is a weak positive correlation between local autonomy and the percentage of the states' population living in the two largest cities. The data comes from the United States Census, 2010.

My second control is the Gini index of income inequality for each state. A Gini index measures the frequency distribution of a data set, in this case income per capita.  An income inequality gap creates conflicting interests between voters and between geographic areas within a state, and is a a disincentive to centralization. As expected, there is a modest positive correlation between local autonomy and income inequality. The data comes from the United States Census, 2010.

The third control is a Sullivan diversity index, which measures the probability that two randomly chosen individuals will have a different ethnic identification. Diversity is a third source of tension that might drive variation in local autonomy. In highly homogeneous states, local autonomy may be unnecessary because the interests and values of all citizens may be relatively closely aligned. By contrast, highly diverse states might lead to political conflict that could result in devolved decision-making to please variable constituencies. (U.S. Mapping Project, 2000).

Descriptive Statistics

	N	Minimum	Maximum	Mean	Std. Deviation
% Pop Communites < 2500	50	.05	.61	.2641	.14567
Income Inequality	50	.412	.535	.45242	.021698
Local Autonomy Index	50	-.982	.845	-.00002	.424178
% Pop Living in 2 Largest Cities	50	.0000	.4611	.166386	.1005144
Diversity	50	.07	.73	.3658	.16408

There were a few interesting observations to be made just from the descriptive statistics. The income inequality range was surprisingly narrow – on a 0 to 1 scale, only .12 separates the minimum from the maximum. The other note about the descriptive table is that the .0000 minimum for the % of the population living in the top two cities represents Vermont – according to the U.S. Census, there are no large cities in Vermont, so it does not list population statistics for them.

Findings

Correlation Matrix – Simple Coefficients

		Local Autonomy	Income Inequality	% Population in Communities < 2500	% Population in Two Largest Cities	Diversity
Pearson Correlation	Local Autonomy	1.000	.075	-.212	.226	.350
	Income Inequality	.075	1.000	-.165	-.182	.211
	% Population in Communities < 2500	-.212	-.165	1.000	-.213	-.618
	% Population in Two Largest Cities	.226	-.182	-.213	1.000	.198
	Diversity	.350	.211	-.618	0.2	1.000
Significance	Local Autonomy	.	.302	.069	.057	.006
	Income Inequality	.302	.	.126	.102	.071
	% Population in Communities < 2500	.069	.126	.	.069	.000
	% Population in Two Largest Cities	.057	.102	.069	.	.084
	Diversity	.006	.071	.000	.084	.

In a simple bivariate correlation test, the uncontrolled Pearson correlation coefficient between the proportion of residents in small communities and the Local Autonomy Index is shown to be slightly negative, but not significant. (r = -.212). Of all the variables, only diversity showed correlations at a level of significance above p = .05. There is a positive correlation between diversity and local autonomy of r = .350 (p = .006), and between diversity and the % population living in small communities of r = -.618 (p = .000). The second diversity correlation is by far the most significant identified in this report.  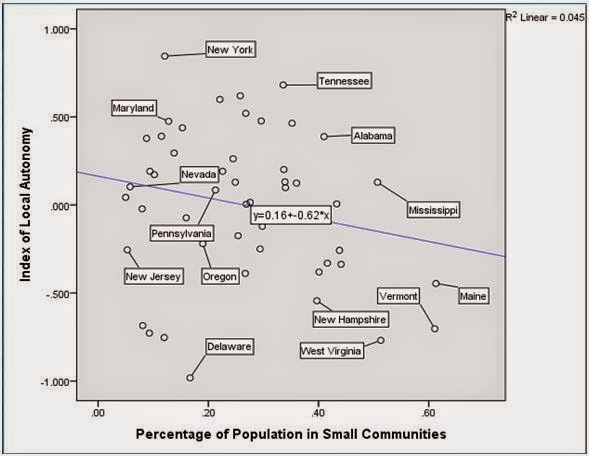Below is the uncontrolled correlation chart showing the relationship between my independent variable, population in small communities, and the Local Autonomy index.

 

% Population in Small Communities and Local Autonomy

Uncontrolled scatter plot with line of best fit

The line suggests a slight negative relationship between population in small communities and local autonomy (the opposite of the hypothesized relationship), but it is not quite statistically significant (p = .069). In a finding that corresponds strongly with Stephens index of centralization (Stephens & Wikstrom, 2007), and as pointed out by Wollman et al (Wollman et al, 2008), the New England states score low on the local autonomy index despite a strong tradition of venerating local government. While Vermont has a centuries-old practice of town meetings, as described in detail by Bryan in 2004, Vermont nonetheless is one of the most centralized governance systems in the United States and its local political units appear to enjoy little decision-making power.

Because two out of three of my control variables (income inequality and the proportion of a states' population concentrated in the two largest cities) did not show a significant relationship with local autonomy, I here show only the results of the primary correlation I am examining controlled for diversity. As you can see from the below chart, the relationship between diversity-controlled autonomy and the percentage of a states' population in small communities is almost exactly zero.

% Population in Small Communities and Diversity-controlled Local Autonomy

The table below shows the controlled coefficients.

Correlations
Control Variables			Local Autonomy	% Pop in Small Communities l
Diversity	Local Autonomy	Correlation	1.000	.005
		Significance (1-tailed)	.	.485
	% Pop in Small Communities	Correlation	.005	1.000
		Significance (1-tailed)	.485	.

A multiple linear regression removes all independent variables but diversity, and returns the following results.

Model Summaryb
Model	R	R Square	Adjusted R Square	Std. Error of the Estimate
1	.350a	.122	.104	.401472
a. Predictors: (Constant), Diversity
b. Dependent Variable: LocalAut

As described earlier, the only positive relationship with local autonomy I was able to identify was diversity. This is shown in the below graph, with a line of best fit and the linear R squared returned by the multiple linear regression above.

Diversity and Local Autonomy

The figure below represents the path analysis for all the variables except diversity.

  

Conclusions & Further Research

I was unable to find a correlation between community size and the degree of local political control in each state. While it's possible that additional controls, different operationalization of "small community" or other adjustments might reveal a correlation, the results of this paper suggest that any relationship is at most modest. The positive benefits of small community size may be outweighed by other factors. Although it’s purely conjecture, I’ll outline several of these factors as areas for future research. In states with a high degree of homogeneity, of which there are many, centralized government may reflect the needs and values of localities well enough that increased local autonomy may provide no improvement. Even in states where current conditions might suggest a trend toward greater autonomy, prevailing historical circumstances at a time when precedents and intergovernmental relationships were defined may have set a mold for political structures that is hard to break.

The only significant relationship between independent variables and my dependent variable is between diversity and local autonomy. The positive correlation is high enough that while it explains only about 12% of the variation, it strongly suggests a role for social and political conflict in determining whether individual states develop devolved political structures with a broader, more powerful role for local governments. Research in the field of local political autonomy mostly began in the 1960s and 1970s in the U.S., and has primarily focused on defining and understanding centralization and autonomy. Stephens, Clark, Joyce & Mullins and others used a variety of fiscal and economic data to describe autonomy in fiscal terms, while Wirt, Bell & Gabler and others have attempted to introduce other elements of local government and to identify correlates with greater autonomy. Wirt compared composite measures of school centralization and their relationship with fiscal centralization, Bell & Gabler studied the effect of economic growth on centralization of state services, and Sokolow compared trends in autonomy with local property tax changes. (Bell, Brunori & Youngman, 2010). But social correlates with local autonomy appears to be a mainly unexplored area; we don’t know what types of socioeconomic and political environments give rise to local autonomy, or allow it to persist over time, and virtually no analysis has been performed on the comparative efficacy (beyond economic efficiency) of centralized vs. locally autonomous governance.

While Vetter (2007) describes constituent feelings and attitudes on local government compared to national and larger subnational units, the question of what type of society best fosters democracy and local government remains unanswered. This is a question that, in my view, has serious implications for international development aid, efforts to promote democracy and attempts to build liberal political principles into government structures (especially in the Middle East, as many governments pursue reorganization in the wake of the Arab Spring). Further research in this area could provide important, timely insights into the interrelationship between democracy and sociopolitical conditions.

Bibliography

Vetter, Anjelika. (2007). Local Politics: A resource for democracy in Western Europe? Plymouth, UK: Lexington Books. (Translated by Antje Matthaus, originally published by Verlag Leske & Budrich, Leverkausen, DE).

Bell, M., Brunori, D. & Youngman, J (2010). The Property Tax and Local Autonomy. Cambridge, MA: Lincoln Institute of Land Policy.

De Tocqueville, Alexis (1835). Democracy in America: Volume 1. Saunders and Otley.

Bryan, F. M. (2004). Real Democracy: The New England Town Meeting and How It Works. Chicago:       University of Chicago Press.

Stephens, G., & Wikstrom, N. (2007). American Intergovernmental Relations:A Fragmented Federal        Policy. New York: Oxford University Press.

Wollman, H., McManmon, R., Bell, M., & Brunori, D. (2008). Comparing Local Government       Autonomy Across States. George Washington Institute of Public Policy, Working Paper.

Richardson, J. J. (2011). Dillon’s Rule is From Mars, Home Rule is From Venus: Local Government          Autonomy and the Rules of Statutory Construction. Publius: The Journal of Federalism, 41(4), 662-685

Clark, G. L. 1984. A theory of local autonomy. Annals of the Association of American

            Geographers 74: 195–208.

United States Census, 2010.

U.S. Mapping Project, 2000. United States Census Bureau.

Other References

Bluestein, Frayda. 2006. Do North Carolina Local Governments Need Home Rule? North Carolina Law Review (1983, republished 2006).

Bowman, Ann; Kearny, R.C. 2012. Are U.S. Cities Losing Power and Authority?Perceptions of Local Government Actors. Urban Affairs Review. (Originally published online at http://uar.sagepub.com/content/48/4/528).

Appendix A: Data

State	% Pop Top 2	Diversity	Pop % Rural	Income Inequality	Local Autonomy
Alabama	0.0875	0.44	0.41	0.47	0.388
Alaska	0.4109	0.51	0.34	0.412	0.098
Arizona	0.3075	0.53	0.1	0.453	0.172
Arkansas	0.0959	0.36	0.44	0.459	-0.258
California	0.1369	0.67	0.05	0.469	0.043
Colorado	0.2021	0.42	0.14	0.455	0.295
Connecticut	0.0767	0.38	0.12	0.482	-0.753
Delaware	0.0789	0.44	0.17	0.436	-0.982
Florida	0.065	0.52	0.09	0.535	0.378
Georgia	0.0641	0.52	0.25	0.471	0.129
Hawaii	0.2479	0.73	0.08	0.465	-0.685
Idaho	0.1832	0.22	0.29	0.43	-0.25
Illinois	0.2255	0.5	0.12	0.429	0.39
Indiana	0.1671	0.25	0.28	0.465	0.015
Iowa	0.1082	0.14	0.36	0.434	0.124
Kansas	0.1948	0.3	0.26	0.427	0.62
Kentucky	0.3084	0.2	0.42	0.444	-0.331
Louisiana	0.1265	0.5	0.27	0.464	0.52
Maine	0.0498	0.07	0.61	0.475	-0.446
Maryland	0.1248	0.53	0.13	0.434	0.475
Massachusetts	0.122	0.32	0.08	0.441	-0.022
Michigan	0.0912	0.36	0.25	0.469	-0.175
Minnesota	0.1259	0.22	0.27	0.449	-0.389
Mississippi	0.0813	0.5	0.51	0.438	0.129
Missouri	0.1301	0.29	0.3	0.474	0.477
Montana	0.1728	0.19	0.44	0.45	-0.337
Nebraska	0.3654	0.23	0.27	0.437	0.004
Nevada	0.3116	0.53	0.06	0.432	0.103
New Hampshire	0.1489	0.1	0.4	0.437	-0.544
New Jersey	0.0597	0.53	0.05	0.421	-0.255
New Mexico	0.3125	0.62	0.23	0.463	0.191
New York	0.4611	0.57	0.12	0.459	0.845
North Carolina	0.1191	0.46	0.34	0.498	0.131
North Dakota	0.248	0.16	0.4	0.463	-0.381
Ohio	0.1026	0.28	0.22	0.444	0.599
Oklahoma	0.2591	0.43	0.34	0.45	-0.033
Oregon	0.1931	0.29	0.19	0.459	-0.22
Pennsylvania	0.1442	0.28	0.21	0.446	0.085
Rhode Island	0.2477	0.32	0.09	0.458	-0.728
South Carolina	0.0539	0.48	0.34	0.456	0.201
South Dakota	0.2725	0.22	0.43	0.461	0.006
Tennessee	0.2007	0.35	0.34	0.44	0.681
Texas	0.1363	0.61	0.15	0.469	0.438
Utah	0.1143	0.26	0.09	0.472	0.191
Vermont	0	0.08	0.61	0.413	-0.703
Virginia	0.0851	0.47	0.25	0.432	0.262
Washington	0.1216	0.37	0.16	0.457	-0.073
West Virginia	0.0277	0.1	0.51	0.441	-0.769
Wisconsin	0.1456	0.23	0.3	0.454	-0.121
Wyoming	0.2036	0.21	0.35	0.429	0.464